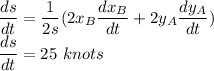Answer:
The chance in distance is 25 knots
Step-by-step explanation:
The distance between the two particles is given by:
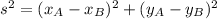 (1)
(1)
Since A is traveling north and B is traveling east we can say that their displacement vector are perpendicular and therefore (1) transformed as:
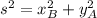 (2)
(2)
Taking the differential with respect to time:
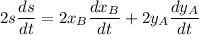 (3)
(3)
where
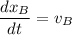 and
and
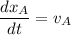 are the respective given velocities of the boats. To find
are the respective given velocities of the boats. To find
 and
and
 we make use of the given position for A,
we make use of the given position for A,
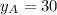 , the Pythagoras theorem and the relation between distance and velocity for a movement with constant velocity.
, the Pythagoras theorem and the relation between distance and velocity for a movement with constant velocity.
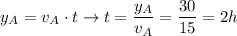
with this time, we know can now calculate the distance at which B is:
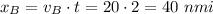
and applying Pythagoras:
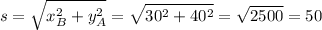
Now substituting all the values in (3) and solving for
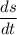 we get:
we get: