Answer:
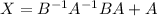
Explanation:
We are given that a matrix equation
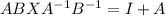
We have to solve the given matrix equation for X.
Suppose all matrix are invertible.
Left multiply by
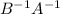 on both sides then ,we get
on both sides then ,we get
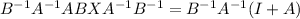
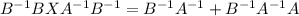
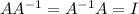 When A is invertible.
When A is invertible.
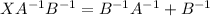 (
(
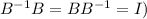
Right multiply by BA on both sides then we get
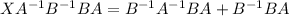
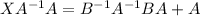
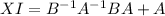
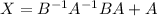 (XI=X)
(XI=X)