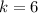Answer:

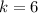
Explanation:
Given:
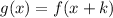
Function transformation rule used:
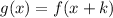
If value of
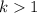 then the graph shifts
then the graph shifts
 units to the left.
units to the left.
If value of
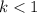 then the graph shifts
then the graph shifts
 units to the right.
units to the right.
From the graph, it is clear that the function
 has moved 6 units(-4 to-10) to the left of
has moved 6 units(-4 to-10) to the left of
 . This shows that the value of
. This shows that the value of
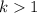 and it is
and it is
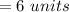
Thus the transformation rule can be given as:

∴