Question

A bowling alley charges its customers an hourly rate to bowl plus shoe rental. The hourly rates are per lane. A linear model of this situation contains the values (2, 34) and (3, 49.25), where x represents the number of hours bowled on one lane, and y represents the total cost for bowling. What is the rate of change in this linear model?

Answer 1

The rate of change in this linear model represents the increase in cost per hour of bowling on one lane. The slope of the line is 15.25.

Step-by-step explanation:

The rate of change in this linear model represents the increase in cost per hour of bowling on one lane. To find the rate of change, we can use the formula for the slope of a line:

slope = (y2 - y1) / (x2 - x1)

Using the given points (2, 34) and (3, 49.25), we can substitute the values into the formula:

slope = (49.25 - 34) / (3 - 2)

= 15.25 / 1

= 15.25.

Answer 2

The rate of change for the linear model = 15.25

Step-by-step explanation:

Given:

A linear model where
`x` represents number of hours bowled on one lane and
`y` represents the total cost of bowling.

`(2,34)`

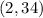
This point shows that the cost of bowling for 2 hours = $34

`(3,49.25)`

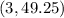
This point shows that the cost of bowling for 3 hours = $49.25

To find the rate of change in the given model we need to find the slope of the line
`m` using the given points.

`m=(y_2-y_1)/(x_2-x_1)`

`m=(49.25-34)/(3-2)`

`m=(15.25)/(1)`

`m=15.25`

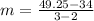
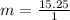
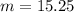
∴ the rate of change for the linear model = 15.25

This shows that the bowling alley charges its customers an hourly rate of $15.25.