Question

A 73-kg person in a moving car stops during a car collision in a distance of 0.80 m . The stopping force that the air bag exerts on the person is 8000 N. Determine the speed of the person before the air bag opens up.

Answer 1

13.24m/s

Step-by-step explanation:

To solve this exercise we go back to the kinematic equations of motion in search of acceleration and the initial speed at which the object was moving.

Once found it will be possible to determine the estimated time.

Our values are:

`F=-8000N`

`m=73Kg`

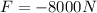
Applying the Second Newton's Law:

`a= (F)/(m)`

`a=(8000)/(73)`

`a = 109.58m/s^2`

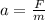
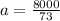
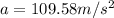
During the collision the distance is 0.8m and there is not final velocity, then

`v_f^2 = v^2_0+2ax`

`0 = v^2_0+2(109.58)(0.8)`

`v_^2_0 = 175.328`

`v_0 = 13.24m/s`

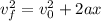
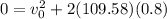
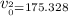
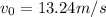
From the Kinetic Equation we have also

`v_f = v_0 - at`

`0 = 13.24-(109.58)t`

`t= 0.1208s`

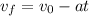
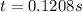
Therefore the velocity before the air bag opens up is 13.24m/s in an interval time of 0.12s to open the air bag

Answer 2

v₀ = 13.24 m / s

Step-by-step explanation:

Let's use Newton's second law to find the average acceleration during the crash

F = m a

. a = F / m

a = 8000/73

a = 109.59 m / s²

Now we can use the kinematic equations to find the initial velocity, since when the velocity stops it is zero (v = 0)

v² = v₀² - 2 a x

v₀² = 2 a x

v₀ = √ 2 a x

v₀ = √ (2 109.59 0.80)

v₀ = 13.24 m / s