Question

A CD has a mass of 17 g and a radius of 6.0 cm. When inserted into a player, the CD starts from rest and accelerates to an angular velocity of 20 rad/s in 0.65 s. Assuming the CD is a uniform solid disk, determine the net torque acting on it.

Answer 1

τ =9.41 * 10⁻⁴ N*m

Step-by-step explanation:

Kinematics of the CD

The CD rotates with constant angular acceleration and its angular acceleration is calculated as follows:

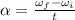`\alpha = (\omega_(f)- \omega_(i))/(t)` Formula (1)

Where:

α : angular acceleration. (rad/s²)

ωf: final angular velocity (rad/s)

ωi : initial angular velocity (rad/s)

t = time interval (s)

Data

ωf= 20 rad/s

ωi =0

t = 0.65 s.

Calculating of the angular acceleration of the CD

We replace data in the formula (1)

`\alpha = (20 -0)/(0.65)`

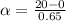
α = 30.77 rad/s²

Newton's second law in rotation:

F = ma has the equivalent for rotation:

τ = I * α Formula (2)

where:

τ : It is the net torque applied to the body. (N*m)

I : it is the moment of inertia of the body with respect to the axis of rotation (kg*m²)

α : It is angular acceleration. (rad/s²)

Calculating of the moment of inertia of the CD

The moment of inertia of a disk with respect to an axis perpendicular to the plane and passing through its center is calculated by the following formula:

I = (1/2) M*R² Formula (3)

Data

M= 17 g = 17/1000 kg = 0.017 kg : CD mass

R= 6.0 cm= 6/100 m = 0.06 m : CD radius

We replace data in the formula (3) :

I = (1/2) ( 0.017 kg)*(0.06 m)² = 3.06 * 10⁻⁵ kg*m²

Calculating of the net torque acting on the CD

Data

α = 30.77 rad/s²

I = 3.06 * 10⁻⁵ kg*m²

We replace data in the formula (2) :

τ = I * α

τ =( 3.06 * 10⁻⁵ kg*m²) * (30.77 rad/s²)

τ =9.41 * 10⁻⁴ N*m