Question

Write a compound inequality to represent all of the numbers between -4 and 6.
PLEASE help

Answer 1

A compound inequality is when it has two inequality sings. This is used to represent intervals, a set of number between two limits. In this case, we need to represent a set of numbers between -4 and 6. It's important to consider that "between" means that -4 and 6 are not included, so we want to represent all numbers more than -4 and less than 6.

So, the first part "all numbers more than -4" can be represented in two ways: x > -4 or -4 < x, both ways represents the same thing, but in this case we are gonna use -4 < x, because it's a compound inequality, where the "x" is always in the middle.

On the other hand, we have "less than 6", this can be also represented in two ways: x < 6 or 6 > x. Now, we need to use the first expression, because to form the compound inequality we need the right side limit.

Therefore, the final compound inequality would be:

-4 < x < 6

Just remember, a compound inequality has a right side limit, and a left side limit. So, in this case the expression is saying considering all numbers between -4 and 6.

Now, we just need to apply an operator that indicates that the compound inequality is for all numbers between those limits. That universal operator is
`\forall`.

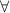At last, the final expression would be:

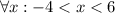`\forall x:-4 < x < 6`.

Answer 2

The compound inequality to represent all numbers between -4 and 6 is,

represented by the set A = -4 ≤ x ≤ 6

Explanation:

The compound inequality to represent all numbers between -4 and 6 is,

represented by the set A = -4 ≤ x ≤ 6.

The above inequality is compound since it involves 2 '≤' symbol.