Question

A new gas- and electric-powered hybrid car has recently hit the market. The distance traveled on 1 gallon of fuel is normally distributed with a mean of 65 miles and a standard deviation of 4 miles. Find the probability of the following events.a. The car travels more than 70 miles per gallon.b. The car travels less than 60 miles per gallon.c. The car travels between 55 and 70 miles per gallon.

Answer 1

Answer: a. 0.1056 b. 0.1056 c. 0.8882

Explanation:

Given : The distance traveled on 1 gallon of fuel is normally distributed with a mean of 65 miles and a standard deviation of 4 miles.

i.e.
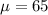`\mu=65` and
`\sigma=4`

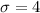
Let x represents the distance traveled on 1 gallon of fuel .

a. The probability that the car travels more than 70 miles per gallon :

`P(x>70)=P((x-\mu)/(\sigma)>(70-65)/(4))\\\\=P(z>1.25)\\\\=1-P(z\leq1.25)\ \ [\because\ P(Z>z)=1-P(Z\leq z)]\\\\=1-0.8944=0.1056`

b. The probability that the car travels less than 60 miles per gallon :

`P(x<60)=P((x-\mu)/(\sigma)<(60-65)/(4))\\\\=P(z<-1.25)\\\\=1-P(z\leq1.25)\ \ [\because\ P(Z<-z)=1-P(Z\leq z)]\\\\=1-0.8944=0.1056`

c. The probability that the car travels between 55 and 70 miles per gallon:

`P(55<x<70)=P((55-65)/(4)<(x-\mu)/(\sigma)<(70-65)/(4))\\\\=P(-2.5<z<1.25)\\\\=P(z<1.25)-P(z<-2.5)\\\\=P(z<1.25)-(1-P(z\leq2.5)\ \ [\because\ P(Z<-z)=1-P(Z\leq z)]\\\\=0.8944-(1-0.9938)=0.8882`