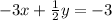Question

What value of b will cause the system to have an infinite number of solutions?

y = 6x + b
-3x+ 1/2 y = -3

Answer 1

b must be equal to -6 for infinitely many solutions for system of equations
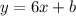`y = 6x + b` and
`-3 x+(1)/(2) y=-3`

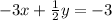
Solution:

Need to calculate value of b so that given system of equations have an infinite number of solutions

`\begin{array}{l}{y=6 x+b} \\\\ {-3 x+(1)/(2) y=-3}\end{array}`

Let us bring the equations in same form for sake of simplicity in comparison

`\begin{array}{l}{y=6 x+b} \\\\ {\Rightarrow-6 x+y-b=0 \Rightarrow (1)} \\\\ {\Rightarrow-3 x+(1)/(2) y=-3} \\\\ {\Rightarrow -6 x+y=-6} \\\\ {\Rightarrow -6 x+y+6=0 \Rightarrow(2)}\end{array}`

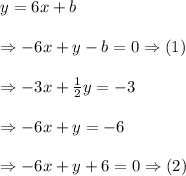
Now we have two equations

`\begin{array}{l}{-6 x+y-b=0\Rightarrow(1)} \\\\ {-6 x+y+6=0\Rightarrow(2)}\end{array}`

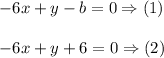
Let us first see what is requirement for system of equations have an infinite number of solutions

If
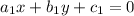`a_(1) x+b_(1) y+c_(1)=0` and
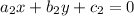`a_(2) x+b_(2) y+c_(2)=0` are two equation

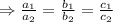`\Rightarrow (a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2))` then the given system of equation has no infinitely many solutions.

In our case,

`\begin{array}{l}{a_(1)=-6, \mathrm{b}_(1)=1 \text { and } c_(1)=-\mathrm{b}} \\\\ {a_(2)=-6, \mathrm{b}_(2)=1 \text { and } c_(2)=6} \\\\ {(a_(1))/(a_(2))=(-6)/(-6)=1} \\\\ {(b_(1))/(b_(2))=(1)/(1)=1} \\\\ {(c_(1))/(c_(2))=(-b)/(6)}\end{array}`

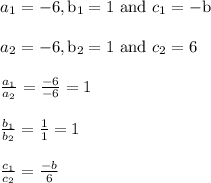
As for infinitely many solutions
`(a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2))`

`\begin{array}{l}{\Rightarrow 1=1=(-b)/(6)} \\\\ {\Rightarrow6=-b} \\\\ {\Rightarrow b=-6}\end{array}`

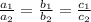
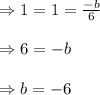
Hence b must be equal to -6 for infinitely many solutions for system of equations
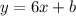`y = 6x + b` and
`-3 x+(1)/(2) y=-3`