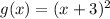Answer:
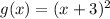
Explanation:
The function that belong to the blue curve, it's the same red curve functions but translated. So, we just need to deduct how was translated.
We observe, that the function was translated to the left and then upwards. To translate in a horizontal direction we have to alter x-variable, to translate in a vertical direction we have to alter y-variable.
So, in this case, the given function is:
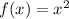
We observe that it was translated three units to the left, that means we have to sum three units to x:
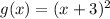
Horizontally, if we sum, we move to the left, if we subtract, we move to the right.
Then, we see that the function was moved one unit upwards:
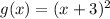
Vertically, if we sum, we move upwards, if we subtract, we move downwards.
Therefore, the translated function is