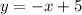For this case we have that by definition, the equation of a line of the slope-intersection form is given by:
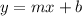
Where:
m: It's the slope
b: It is the cut-off point with the y axis
The slope can be found using the formula:
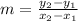
We have the following points:
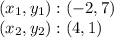
Thus, the slope is:
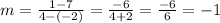
Thus, the equation is of the form:
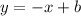
We substitute a point and find "b":
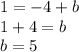
Finally, the equation is:
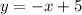
Answer: