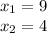For this case we have the following function:
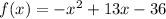
To find the zeros of the function we make
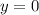 and solve for "x", then:
and solve for "x", then:
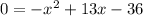
We multiply by -1 on both sides of the equation:
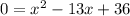
We factor the equation, for this we look for two numbers that, when multiplied, result in 36 and when added, result in -13. These numbers are -9 and -4.

Thus, the factored equation is:
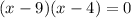
Therefore, the roots are:
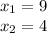
Answer: