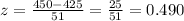Answer:
(a) -3.708
(b) 1.706
(c) 0.490
Explanation:
The z-score of normal distribution is given as:

(a)
Given:
Score is,
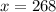
Mean value is,
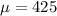
Standard deviation is,

z-score is,
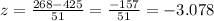
(b)
Given:
Score is,
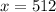
Mean value is,
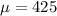
Standard deviation is,

z-score is,
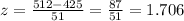
(c)
Given:
Score is,
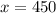
Mean value is,
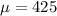
Standard deviation is,

z-score is,