Answer:
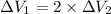
Step-by-step explanation:
The bulk modulus is a constant that describes how resistant a substance is to compression.
It is defined as the ratio between increase in pressure and the resulting decrease in a volume of the material.
It is given by a formula :
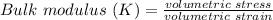
OR

where:
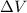 &
&
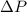 are the change in volume and change in pressure respectively.
are the change in volume and change in pressure respectively.
V= original volume
According to the given:

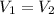
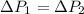
So,
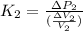
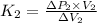 .................................(1)
.................................(1)
&
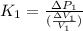
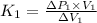 ..................................(2)
..................................(2)
From the given conditions we compare equations (1) & (2):

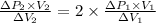
cancelling the equal terms
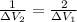
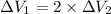
The material in first case undergoes twice the volume reduction than that of the material in first case under the given conditions.