Question

Two 1.50-V batteries—with their positive terminals in the same direction—are inserted in series into the barrel of a flashlight. One battery has an internal resistance of 0.320 Ω, the other an internal resistance of 0.140 Ω. When the switch is closed, a current of 600 mA occurs in the lamp. (a) What is the bulb's resistance?

Answer 1

`R=4.54\ \Omega`

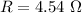
Step-by-step explanation:

It is given that,

Voltage of the battery, V = 1.5 V

Internal resistance of battery 1,
`r_1=0.32\ \Omega`

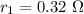
Internal resistance of battery 2,
`r_2=0.14\ \Omega`

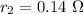
Current flowing in the lamp,
`I=600\ mA=600* 10^(-3)\ A=0.6\ A`

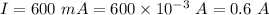
Total internal resistance of tow batteries,

`r=r_1+r_2`

`r=0.32+0.14`

`r=0.46\ \Omega`

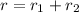
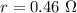
Let R is the resistance of the bulb. Let V is the total emf of the circuit. It is given by :

`V=I(R+r)`

`R=(V)/(I)-r`

`R=(2* 1.5)/(0.6)-0.46`

`R=4.54\ \Omega`

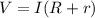
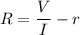
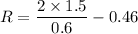
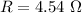
So, the resistance of the bulb is 4.54 ohms. Hence, this is the required solution.