Answer:
The expected time for Bob to get to school today is 34 minutes.
Explanation:
We have these following probabilities:
A 70% probability that Sam sleeps through Bob's phone call and does not answer this morning. In this case, Bob has to walk to school. Bob is a consistent walker, and will always make it to school in exactly 40 minutes.
A 30% probability that Sam answers the phone. If Sam answers the phone, he will drive to Bob's house and give Bob a ride. Bob will get to school in X minutes, where X follows a (continuous) Uniform(15,25) distribution. In this case of an Uniform distribution, the expected time is (15+25)/2 = 20 minutes.
What is the expected time for Bob to get to school today (in minutes)?
There is a 70% probability it takes 40 minutes for Bob to get to school and a 30% probability it takes him 20 minutes. So:
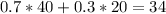
The expected time for Bob to get to school today is 34 minutes.