Question

Describe the relationship between the pressure and volume of a gas when temperature and mass are constant

Answer 1

The product of Pressure and Volume is a constant.

Step-by-step explanation:

We know the Ideal gas equation,

PV = nRT,

where,

P - Pressure of the gas

V - Volume of the gas

n - No. of moles of the gas taken

R - Universal Gas Constant.

T - Temperature of the gas.

We know that , n =
`(wt)/(Mwt)`

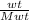
where, wt - Mass of gass ; Mwt - Molecular weight of the gas.

We are given the weight of the gas remains constant (wt is a constant)

Therefore as n =
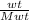`(wt)/(Mwt)`,(where both wt and Mwt are constants)

n is a constant in this process.

Universal gas constant is a constant

Given temperature is a constant.

Therefore,

As, PV = nRT, (where n,R,T are constants),

PV is a constant.

Therefore we can say,

PV = k, for some constant k.

If we plot a graph for P vs V , we get a Rectangular Hyperbola( One of the general forms of a Rectangular Hyperbola is xy = c)