Question

Suppose 75% of all drivers wear their seat belts. Lets investigate how many of the drivers might be belted among five cars waiting at a traffic light. (a) Describe how you would simulate the number of seat belt wearing drivers among the five cars.

Answer 1

The expected number of seat belt wearing drivers among the five cars is 3.75, using the expected value of a binomial experiment.

Explanation:

For each driver, there are only two possible outcomes. Either they wear their seatbelts, or they do not. This means that we solve this problem using concepts of the binomial probability distribution.

Binomial probability disitribution.

Probability of exactly x sucesses on n repeated trials, with p probability.

Has an expected value of:

`E(X) = np`.

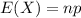(a) Describe how you would simulate the number of seat belt wearing drivers among the five cars.

You would simulate this number finding the expected value of the binomial experiment.

There are 5 cars, so
`n = 5`.

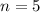75% of all drivers wear their seat belts, so
`p = 0.75`.

So the expected number of seat belt wearing drivers among the five cars is:

`E(X) = np = 5*0.75 = 3.75`

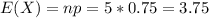
The expected number of seat belt wearing drivers among the five cars is 3.75, using the expected value of a binomial experiment.