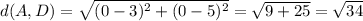Question

1. A quadrilateral has vertices A(0,0), B(8,0),C(7,5), and

D(3,5). 40 points
b. Find the length of each side to the nearest tenth of a
unit.​

Answer 1

The formula for the distance between two points is

`d(A,B) = √((A_x-B_x)^2+(A_y-B_y)^2)`

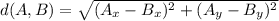
Note that, if two points have one coordinate in common, this formula simplifies to

`d(A,B) = |A_x-B_x|,\quad d(A,B)=|A_y-B_y|`

(the first if they share the y coordinate, the second if they share the x coordinate).

So, these are the lengths of the sides:

`d(A,B)=|8-0|=8`

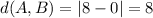
(because they share the y coordinate)

`d(B,C) = √((8-7)^2+(0-5)^2)=√(1+25)=√(26)`

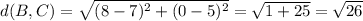
(standard formula)

`d(C,D)=|7-3|=4`

(because they share the y coordinate)

`d(A,D) = √((0-3)^2+(0-5)^2)=√(9+25)=√(34)`