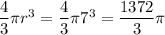Question

PLEASE HELP ASAP

THANK YOU

1. find the area of the composite figure.

40 units2

38.5 units2

39.75 units2

44 units2

#2: The cylinder below needs to be spray-painted. Find the surface area and use π = 3.14. Round to nearest hundredth.

282.62 cm2

207.24 cm2

226.08 cm2

304.25 cm2

#3:
What is the volume of a sphere with a surface area of 196 π ft2 ?

1372/ 3 π ft3

457/ 3 π ft3

226/ 3 π ft3

420 π ft3

Answer 1

1: Refer to the attached image. We can split the composite figure in easy figures: triangles ABC and CDE have a base AC=4 and height of 3. Their area is thus

`A_(ABC)=A_(CDE)=(4\cdot 3)/(2)=6`

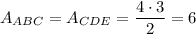
Rectangle AEFH has sides AE=8 and AH=3. So, it has area

`A_(AEFH)=8\cdot 3=24`

Finally, triangle FGH has a base HG=2 and height HF=8. So, its area is

`A_(FGH)=(2\cdot 8)/(2)=8`

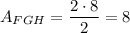
So, the total area is

`A_(ABC)+A_(CDE)+A_(AEFH)+A_(FGH)=6+6+24+8=44`

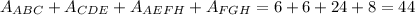
2:

The base radius is 3, so the base area is

`\pi 3^2 = 9\pi`

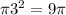
The lateral area is the product between the height and the base circumference:

`9\cdot 6\pi=54\pi`

So, the total area is twice the base area plus the lateral area:

`54\pi+18\pi=62\pi\approx 72\cdot 3.14=226.08`

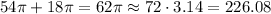
3:

The surface area of a sphere is

`S=4\pir^2`

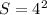
Solving for r, we have

`r=\sqrt{(S)/(4\pi)}=\sqrt{(196\pi)/(4\pi)}=√(49)=7`

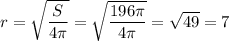
The volume of a sphere is

`(4)/(3)\pi r^3 = (4)/(3)\pi 7^3=(1372)/(3)\pi`