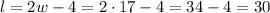Question

Joe has a rectangular chicken coop. The length of the coop is 4 feet less than twice the width. The area of the chicken coop is 510 square feet. What is the length of the chicken coup?

Solve this using the method Table of Values showing each step by step

PLEASE HELP ME I ONLY HAVE SO MUCH TIME!!! THIS IS WORTH 14 POINTS!

Answer 1

Let w and l be the dimensions (width and length, respectively) of the coop.

We know that the length of the coop is 4 feet less than twice the width, which means that

`l=2w-4`

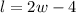
Also, the area is 510, but the area is the product of the dimensions, so we have

`lw=510`

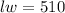
Plug the expression for l in the formula for the area:

`lw=(2w-4)w=510 \iff 2w^2-4w-510=0`

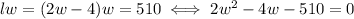
We can divide the whole expression by 2 and solve it with the quadratic formula:

`w^2-2w-255=0 \iff w=(2\pm√(4+1020))/(2)=(2\pm 32)/(2)=1\pm 16`

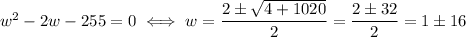
So, the two solutions are

`w_1=1-16=-15,\quad w_2=1+16=17`

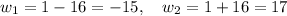
The negative solution makes no sense (we can't have negative lengths), so the width must be 17.

We conclude that the length is

`l=2w-4=2\cdot 17-4=34-4=30`