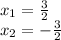Question

16x² -9 = 4ײ + (4x²+9)

Answer 1

For this case we must solve the following equation:

`16x ^ 2-9 = 4x ^ 2 + (4x ^ 2 + 9)`

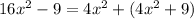
We remove the parentheses on the right side:

`16x ^ 2-9 = 4x ^ 2 + 4x ^ 2 + 9`

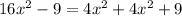
We add similar terms on the right side:

`16x ^ 2-9 = 8x ^ 2 + 9`

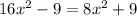
We subtract
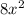`8x ^ 2`from both sides of the equation:

`16x ^ 2-8x ^ 2-9 = 9\\8x ^ 2-9 = 9`

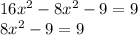
We add 9 to both sides of the equation:

`8x ^ 2 = 9 + 9\\8x ^ 2 = 18`

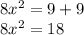
We divide by 8 on both sides of the equation:

`x ^ 2 = \frac {18} {8}\\x ^ 2 = \frac {9} {4}`

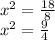
We apply square root to both sides of the equation:

`x = \pm \sqrt {\frac {9} {4}}`

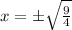
We have two roots:

`x_ {1} = \frac {3} {2}\\x_ {2} = - \frac {3} {2}`

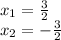
Answer:

`x_ {1} = \frac {3} {2}\\x_ {2} = - \frac {3} {2}`