Answer:
2071
Explanation:
Since, the decline model follows exponential- decay model
thus,

Here,
P₀ is the initial consumption
t is the time in years
P is the consumption after t years
k is the decay constant
now,
1985 is the base year, thus for year 1985; t = 0
at t = 0, P = 80
Therefore,
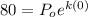
or
P₀ = 80 pounds
also,
in the year 1996 i,e t = 1996 - 1985 = 11 years
P = 67 pounds
thus,
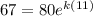
or
0.8375 =

taking the log both sides, we get
-0.177 = 11k
or
k = - 0.01612
Therefore,
For P = 20 pounds per person
we have
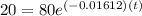
or
0.25 =
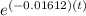
taking natural log both the sides, we get
-1.3863 = (- 0.01612 )(t)
or
t = 85.99 ≈ 86 years
Hence,
the year will be 1985 + 86 = 2071