Answer:
b) Betelgeuse would be
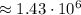 times brighter than Sirius
times brighter than Sirius
c) Since Betelgeuse brightness from Earth compared to the Sun is
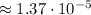 the statement saying that it would be like a second Sun is incorrect
the statement saying that it would be like a second Sun is incorrect
Step-by-step explanation:
The start brightness is related to it luminosity thought the following equation:
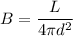 (1)
(1)
where
 is the brightness,
is the brightness,
 is the star luminosity and
is the star luminosity and
 , the distance from the star to the point where the brightness is calculated (measured). Thus:
, the distance from the star to the point where the brightness is calculated (measured). Thus:
b)
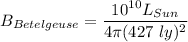 and
and
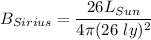 where
where
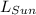 is the Sun luminosity (
is the Sun luminosity (
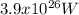 ) but we don't need to know this value for solving the problem.
) but we don't need to know this value for solving the problem.
 is light years.
is light years.
Finding the ratio between the two brightness we get:
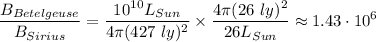
c) we can do the same as in b) but we need to know the distance from the Sun to the Earth, which is
 . Then
. Then
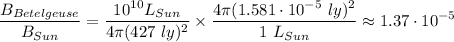
Notice that since the star luminosities are given with respect to the Sun luminosity we don't need to use any value a simple states the Sun luminosity as the unit, i.e 1. From this result, it is clear that when Betelgeuse explodes it won't be like having a second Sun, it brightness will be 5 orders of magnitude smaller that our Sun brightness.