Answer:
Part (A): The required inequality is T < 35 or t >40.
Part (B): The correct option is C) Only x=7.
Part (C) |x+1|+5=2 has no solution; |4x+12|=0 has one solution; |3x|=9 has two solution.
Explanation:
Consider the provided information.
Part (A)
Storing milk at temperatures colder than 35°F can affect its quality of taste. However, storing milk at temperatures warmer than 40°F is an unsafe food practice.
The union is written as A∪B or “A or B”.
The intersection of two sets is written as A∩B or “A and B”
We need to determine the inequalities represent the union of these improper storage.
That means we will use A∪B or “A or B”.
The improper storage temperatures is when temperature is less than 35°F or greater than 40°F.
Hence, the required inequality is T < 35 or t >40.
Part (B) 15| x-7|+4=10|x-7|+4
Solve the inequality as shown below:
Subtract 4 from both sides.
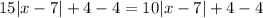
Subtract 10|x-7| from both sides
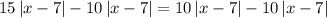

Hence, the correct option is C) Only x=7.
Part (C) Match the solution,
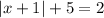
Subtract 2 from both sides.
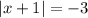
Absolute value cannot be less than 0.
Hence, |x+1|+5=2 has no solution.
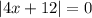


Hence, |4x+12|=0 has one solution.
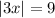

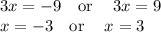
Hence, |3x|=9 has two solution.