Answer:
Given below
Explanation:
Given that population mean = 1500 and population std dev σ = 3.0.
Since sigma is known, we can use z critical values for finding out confidence intervals
a) 95% CI for μ when N = 25 and sample mean = 58.3
=
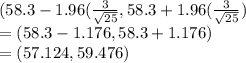
b) a 95% CI for μ when N = 100 and sample mean = 58.3.
=
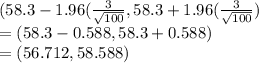
c) a 99% CI for μ when N = 100 and sample mean = 58.3.
=
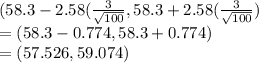
d) a 82% CI for μ when N = 100 and sample mean = 58.3.
=
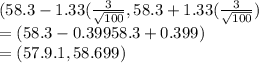
e)
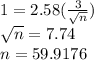
n =60