Question

A confidence interval is desired for the true average stray-load loss μ (measured in watts) for a certain type of induction motor when the line current is held at 10 amps for a speed of 1500 rpm. Assume that the stray-load loss is normally distributed with σ = 3.0.

(a) Compute a 95% CI for μ when N = 25 and sample mean = 58.3.

(b) Compute a 95% CI for μ when N = 100 and sample mean = 58.3.

(c) Compute a 99% CI for μ when N = 100 and sample mean = 58.3.

(d) Compute a 82% CI for μ when N = 100 and sample mean = 58.3.

(e) How large must N be if the width of the 99% CI for μ is to be 1.0?

Expert Answer

Answer 1

Given below

Explanation:

Given that population mean = 1500 and population std dev σ = 3.0.

Since sigma is known, we can use z critical values for finding out confidence intervals

a) 95% CI for μ when N = 25 and sample mean = 58.3

=
`(58.3-1.96((3)/(√(25) ) ,58.3+1.96((3)/(√(25) ))\\= (58.3-1.176, 58.3+1.176)\\= (57.124, 59.476)`

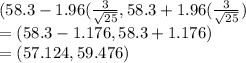
b) a 95% CI for μ when N = 100 and sample mean = 58.3.

=
`(58.3-1.96((3)/(√(100) ) ,58.3+1.96((3)/(√(100) ))\\= (58.3-0.588, 58.3+0.588)\\= (56.712, 58.588)\\`

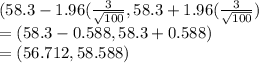
c) a 99% CI for μ when N = 100 and sample mean = 58.3.

=
`(58.3-2.58((3)/(√(100) ) ,58.3+2.58((3)/(√(100) ))\\= (58.3-0.774, 58.3+0.774)\\= (57.526, 59.074)`

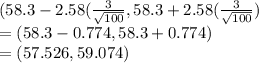
d) a 82% CI for μ when N = 100 and sample mean = 58.3.

=
`(58.3-1.33((3)/(√(100) ) ,58.3+1.33((3)/(√(100) ))\\= (58.3-0.399 58.3+0.399)\\= (57.9.1, 58.699)`

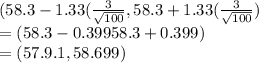
e)
`1=2.58((3)/(√(n) ) )\\√(n) =7.74\\n=59.9176`

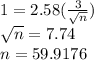
n =60