Question

An aircraft component is fabricated from an aluminum alloy that has a plane-strain fracture toughness of 40 MPa1m (36.4 ksi1in.). It has been determined that fracture results at a stress of 300 MPa (43,500 psi) when the maximum (or critical) internal crack length is 4.0 mm (0.16 in.). For this same component and alloy, will fracture occur at a stress level of 260 MPa (38,000 psi) when the maximum internal crack length is 6.0 mm (0.24 in.)

Answer 1

The material will be fracture.

Step-by-step explanation:

To develop the problem it is necessary to take into account the concepts related to critical stress crrack propagation and the strain fracture toughness at the critical stress.

The half lenght of the internal crack is:

`\alpha = (L)/(2)`

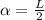
Where L is the length of surface crack, then

`\alpha = (4)/(2)`

`\alpha = 2*10^(-3)m`

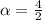
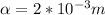
For definition we know that the critical stress crack propagation equation is given by,

`\sigma_c = (K_(lc))/(Y√(\pi \alpha))`

`Y = (K_(lc))/(\sigma_c √(\pi \alpha))`

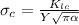
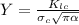
Where,

Y = Dimensionless parameter

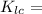`K_(lc) =`Plane strain fracture toughness

`\sigma_c =` critical stress required for initial crack propagation

Our values are given by,

`K_(lc) = 40Mpa√(m)`

`\sigma_c = 300MPa`

`\alpha = 2*10^(-3)m`

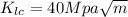
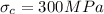
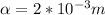
Replacing the values we have:

`Y = (K_(lc))/(\sigma_c √(\pi \alpha))`

`Y = \frac{40}{(300) \sqrt{\pi* 2*10^(-3)}}`

`Y = 1.682`

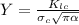
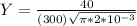
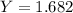
It is now possible to calculate the plane strain fracture toughness at the maximum internal crack length of 6mm, then

`\alpha'=(L')/(2)`

`\alpha' =(6)/(2)`

`\alpha = 3*10^(-3)m`

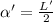
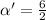
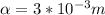
Then from the previous equation given we can calculate the plane strain fracture toughness,

`\sigma_c = (K_(lc))/(Y√(\pi \alpha'))`

`K_(lc) = \sigma_cY√(\pi \alpha')`

`K_(lc) = (260)(1.682))\sqrt{\pi*3*10^(-3)}`

`K_(lc) = 42.455Mpa√(m)`

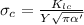
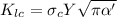
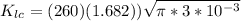
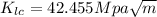
We can conclude that the fracture toughness at maximul lenght of 6mm is
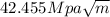`42.455Mpa√(m)` a value higher than the value of the fracture toughness of the material that is
`40MPa \sqrt {m}`

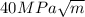
The material will fracture with that conditions