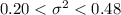Question

A frozen food company uses a machine that packages blueberries in seven pound portions. A sample of 7373 packages of blueberries has a variance of 0.300.30. Construct the 99%99% confidence interval to estimate the variance of the weights of the packages prepared by the machine. Round your answers to two decimal places.

Answer 1

Answer:
`0.20<\sigma^2<0.48`

Explanation:

Given : A A sample of 73 packages of blueberries has a variance of 0.30.

i.e. n= 73 and
`s^2=0.30`

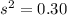
Confidence level:
`\alpha=0.99`

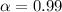
⇒Significance level :
`\alpha=1-0.99=0.01`

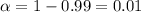
Critical values using chi-square distribution:-

`\chi^2_(\alpha/2, n-1)=\chi^2_(0.005, 72)=106.65`

`\chi^2_(1-\alpha/2, n-1)=\chi^2_(0.995, 72)=44.84`

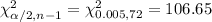
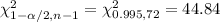
99% confidence interval for population variance will be :-

`(s^2(n-1))/(\chi^2_(\alpha/2, n-1))<\sigma^2<(s^2(n-1))/(\chi^2_(1-\alpha/2, n-1))\\\\\\((0.30)(72))/(106.65)<\sigma^2<((0.30)(72))/(44.84)\\\\ \approx0.20<\sigma^2<0.48`

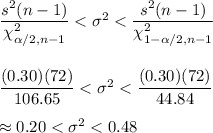
Hence, the 99% confidence interval to estimate the variance of the weights of the packages prepared by the machine:
`0.20<\sigma^2<0.48`