Answer:
The line equation that passes through the given points is 7x – y = 13
Step-by-step explanation:
Given:
Two points are A(2, 1) and B(3, 8).
To find:
The line equation that passes through the given two points.
Solution:
We know that, general equation of a line passing through two points (x1, y1), (x2, y2) in point slope form is given by
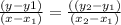
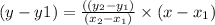 ..........(1)
..........(1)
here, in our problem x1 = 3, y1 = 8, x2 = 2 and y2 = 1.
Now substitute the values in (1)
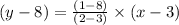
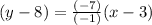
y – 8 = 7(x – 3)
y – 8 = 7x – 21
7x – y = 21 – 8
7x – y = 13
Hence, the line equation that passes through the given points is 7x – y = 13