Answer:
Part 1) The slope of JK is
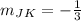
Part 2) The slope of KL is

Part 3) The slope of JL is
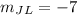
Part 4) Triangle JKL is a right triangle because two of these slopes have a product of -1
Explanation:
we know that
If two lines are perpendicular, then their slopes are opposite reciprocal (the product of their slopes is equal to -1)
The formula to calculate the slope between two points is equal to
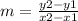
we have
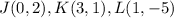
Part 1) Find the slope JK
we have
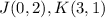
substitute in the formula
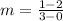
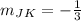
Part 2) Find the slope KL
we have

substitute in the formula
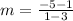
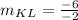

Part 3) Find the slope JL
we have
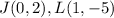
substitute in the formula
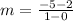
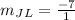
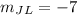
Part 4) Compare the slopes
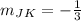

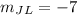
we have that
JK and KL are perpendicular because their slopes are opposite reciprocal
The product of their slopes is equal to -1
therefore
Triangle JKL is a right triangle because two of these slopes have a product of -1