Question

A helical compression spring made of hard-drawn 2mm spring steel wire has an OD of 22mm and 8.5 total coils with plain/ground ends. For the spring to be solid-safe, what are the spring rate k, solid force Fs, and free length L0? Does the spring need to be supported against buckling?

Answer 1

k = 2463 N/m

Fs = 81.12 N

Lo = 47.7 mm

Step-by-step explanation:

given data:

d =2 mm

OD = 22 mm

N_2 = 8.5

from data book

A = 1783 MPa

n = 0.19

`S_[ut] = (1783)/(2^(0.19)) = 1563 MPa`

`S_{sy] = 0.45 S_(ut)  = 70.3.4 MPa`

D = OD - d = 20 mm

c = 2D/2 = 10

`K_b =(4c +2)/(4c  -3) = (4(10) +2)/(4(10) + 3) = 1.135`

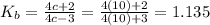
Na = 8.5 -1 = 7/5 turns

`Ls = 2* 6.5 = 17 mm`

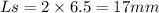
for solid safe use ns = 1.2

spring rate
`k = (Gd^4)/(8D^3 Na) = (79.3* 10^9 (2^4 * 10^(-12))/(8* (20^3 * 10^(-9) * (7.5))`

k = 2463 N/m

solid force

`Fs = (\pi d^3 (S_(sy)/ns) )/(8 Kb D)`

`Fs =(\pi (2^3 * 10^(-19) (703.4* 10^6)/1.2)/(8* 1.135* 20* 10^(-3))`

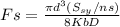
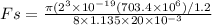
Fs = 81.12 N

Free length

`Lo = y + Ls = (Fs)/(k) + Ls = (81.12)/(2463* 10^(-3))  + 17 = 47.7 mm`

`Lo_(et) = (2.63 D)/(\alpha) = (2.63* 20)/(0.5) = 105.2`

`(LO_(et))/(Lo) = (105.2)/(47.7) = 2.2`

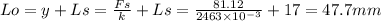
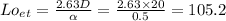
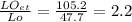
As Lo is less than 105.2 the spring wiill not be buckle