Question

A disk rotates at constant angular acceleration, from angular position θ1 = 16.0 rad to angular position θ2 = 76.0 rad in 5.30 s. Its angular velocity at θ2 is 11.0 rad/s.

(a) What was its angular velocity at θ1?
(b) What is the angular acceleration?
(c) At what angular position was the disk initially at rest?

Answer 1

(a) the angular velocity at θ1 is 11.64 rad/s

(b) the angular acceleration is 0.12 rad/
`s^(2)`

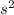
(c) the angular position was the disk initially at rest is - 428.27 rad

Step-by-step explanation:

Given information :

θ1 = 16 rad

θ2 = 76 rad

ω2 = 11 rad/s

t = 5.3 s

(a) The angular velocity at θ1

First, we use the angular motion equation for constant acceleration

Δθ = (ω1+ω2)t/2

θ2 - θ1 = (ω1+ω2)t/2

ω1 + ω2 = 2 (θ2 - θ1) / t

ω1 = (2 (θ2 - θ1) / t ) - ω2

= (2 (76-16) / 5.3) - 11

= 11.64 rad/s

(b) the angular acceleration

ω2 = ω1 + α t

α t = ω2 - ω1

α = (ω2 - ω1)/t

= (11.64 - 11) / 5.3

= 0.12 rad/
`s^(2)`

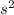
(c) the angular position was the disk initially at rest, θ0

at rest ω0 = 0

ω2^2 = ω01 t + 2 α Δθ

2 α Δθ = ω2^2

θ2 - θ0 = ω2^2 / 2 α

θ0 = θ2 - (ω2^2) / 2 α

= 76 - (
`11^(2)`/ 2 x 0.12

= 76 - 504.16

= - 428.27 rad