Answer:
The rate of interest for the investment is 3.8
Explanation:
Given as :
The Principal = 1500 unit
The Amount after 3 years = 1680 unit
The Time period = 3 years
Let The annual rate of interest = R %
From compounded method
Amount = Principal ×
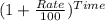
Or, 1680 = 1500 ×
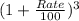
Or,
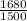 =
=
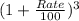
Or, 1.12 =
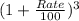
Or,
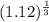 = 1 +
= 1 +
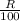
Or, 1.038 = 1 +
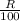
So, 1.038 - 1 =
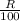
∴ 0.038 × 100 = R
I.e R = 3.8
Hence The rate of interest for the investment is 3.8 Answer