Question

Joanna set a goal to drink more water daily. The number of ounces of water she drank each of the last seven days is shown below. 60, 58, 64, 64, 68, 50, 57. On the eighth day, she drinks 82 ounces of water.

Select all the true statements about the effect of the eighth day's amount on Joanna's daily amount distribution.

The average daily amount of water is the same with or without the inclusion of the eighth day's amount.

The median amount of water is the same with or without the inclusion of the eighth day's amount.

The interquartile range of the data decreases when the eighth day's amount is included in the data.

The interquartile range of the data increases when the eighth day's amount is included in the data.

The median amount of water is higher when the eighth day's amount is included in the data.

Answer 1

The median amount of water is higher when the eighth day's amount is included in the data.

The interquartile range of the data increases when the eighth day's amount is included in the data.

Explanation:

IQR with 8th day: 8.5

Before 8th day= 7

Median with 8th day= 62

before 8th day=60

Answer 2

The median amount of water is higher when the eighth day's amount is included in the data.

Step-by-step explanation:

Given the ounces of water drank is 60, 58, 64, 64, 68, 50, 57

Arranging in ascending order: 50, 57, 58, 60, 64, 64, 68

Calculating the median of the above data

Median (when n is odd) =
`\left((n+1)/(2)\right)^(t h) \text { term }`

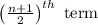
where n =7

Median = 4th term = 60

When the eight day is added,

Series will be: 50, 57, 58, 60, 64, 64, 68, 82

Median (when n is even) =
`(\left((n)/(2)\right)^(t h) t e r m+\left((\pi)/(2)+1\right)^(t h) t e r m)/(2)`

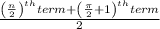
Median =
`(60+64)/(2)=62`

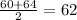
So, here we can say that median has increased after adding 82 in the data