Question

A researcher was interested in studying americans email habits. She suspected that americans spend less than 7 hours a week answering their email.The general social survey in 2004 included a question that asked about the number of hours that the respondent spend on email per week.The general social survey in 2000 asked 783 respondents this question. The sample mean number of hours was 5.54 and the sample standard deviation was 7.23. Find the test statistic.

Answer 1

Answer: t=-5.651

Step-by-step explanation:

Let
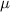`\mu` be the population mean number of hours a week answering their email.

As per given we have

`H_0: \mu\geq7\\\\ H_a: \mu <7`

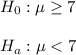
Sample size : n= 783

Sample mean :
`\overline{x}=5.54`

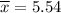
Sample standard deviation: s=7.23

Since population standard deviation is unknown, so our test -statistic has a t-distribution.

Test statistic :
`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

`=(5.54-7)/((7.23)/(√(783)))\\\\\\=(-1.46)/(0.2583791)\\\\\approx-5.651`

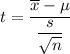
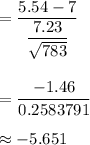
∴ The test statistic : t=-5.651