Question

As a student technician, you are preparing a lecture demonstration on "magnetic suspension." You have a 15-cm long straight, rigid wire that will be suspended by flexible conductive lightweight leads above a long, straight wire. Currents that are equal but are in opposite directions will be established in the two wires so the 15-cm wire "floats" a distance h above the long wire with no tension in its suspension leads. If the mass of the 15-cm wire is 13.4 g and if h (the distance between the central axes of the two wires) is 1.5 mm, what should their common current be?

Answer 1

I = 81.0721 A

Step-by-step explanation:

There are two force that are acting on wire i.e. upward magnetic force and weight of body itself

considering the equilibrium condition

Apply
`\sum F` in vertical direction is 0 thus we have

F_B - mg = 0

repulsive that acting oin wire is

`F_b = 2[(\mu_o I^2 L)/(4\pi R)]`

Plugging this value tn above equation

`2[(\mu_o I^2 L)/(4\pi R)] - mg  = o`

solving for current I

`I = \sqrt{(4\pi R mg)/(2\mu_o L)}`

`I = \sqrt{(13.4* 10^(-3)9.81(1.5* 10^(-3))/(2(10^(-7) T.m/A (.15m))}`

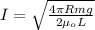
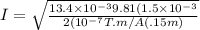
I = 81.0721 A