Question

On an elementary school examination in spelling, the mean grade of 32 boys was 72 with a standard deviation of 8, while the mean grade of 36 girls was 75 with a standard deviation of 6. Test the hypothesis at a (a) 0.05, (b) 0.01 level of significance that the girls are better in spelling than the boys

Answer 1

For Part A:

Z>Z_{0.05} hence reject H₀ it means girls are better.Hₐ hypothesis is correct

For Part B:

Z<Z_{0.01} hence Girls are not better and Hₙ hypothesis is correct.

Explanation:

Consider the Two Hypothesis:

H₀:
`u_(G)`=
`u_(B)`

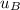
Hₐ:
`u_(G)`>
`u_(B)`

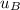
Hₙ:
`u_(G)`<
`u_(B)`

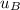
Test Statistics:

Z=
`\frac{(x_(G) -x_(B) )-(u_(G)-u_(B))  }{\sqrt{(S_(G) ^(2) )/(n_(G) )+(S_(B)^(2) )/(n_(B) )  } }`

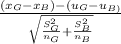
Where

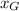`x_(G)` is the mean grade of girls

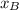`x_(B)` is the mean grade of boys

`S_(G)` is the standard deviation of girls

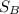`S_(B)` is the standard deviation of boys

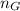`n_(G)` is the number of girls

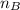`n_(B)` is the number of boys

Z=
`\frac{(75 -72 )-0  }{\sqrt{(6^(2) )/(36 )+(8^(2) )/(32 )  } }`

Z≅1.73

Critical Value at
`Z_(0.05) = 1.645\\Z_(0.01) = 2.326`

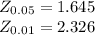
For Part A:

Z>Z_{0.05} hence reject H₀ it means girls are better.Hₐ hypothesis is correct

For Part B:

Z<Z_{0.01} hence Girls are not better and Hₙ hypothesis is correct.