Answer:
Part A:
n=6591.87≅6592
Part B:
n=6765.06≅6765
Explanation:
In order to calculate the sample size we use the following estimated Sample proportion formula:
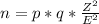
Where:
p is the previous estimate
q is the 1-p
Z is the distribution
E is the margin
At 90% Confidence significance level is 0.1/2=0.05
Z at 0.05 or 5% =1.645
Part A:
p=0.42
q=1-p=1-0.42=0.58
Z=1.645
E=0.01
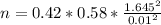
n=6591.87≅6592
Part B:
Since no prior estimate is given we assume p =0.5 and q=0.5
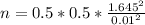
n=6765.06≅6765