Answer:
J = 2.044x10⁶ A/m²
v = 1.50x10⁻⁴ m/s
Explanation:
The current density (J) of the copper wire is giving by:

where I: electric current and A: cross-sectional area of the copper wire
The cross-sectional area of the copper wire can be calculated by:
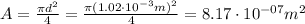
Substituting the calculated area in the equation (1) we have:
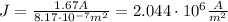
Hence, the current density is 2.044x10⁶ A/m².
To find the drift speed (v), we need to use the next equation:
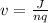
where n: the free-electron density, q: module of the charge of the electron
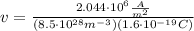
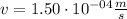
So, the drift speed is 1.50x10⁻⁴ m/s.
Have a nice day!