Question

At a restaurant, 80 percent of the diners are new customers P(N)=0.8, while 20 percent are regular customers P(N’)=0.2. And, 50 percent of the new customers pay by credit card P(C|N)=0.5, in contrast, 70 percent of the regular customers make payments by credit card P(C|N’)=0.7. What is the probability that a customer is new if he/she pays by credit card, P(N|C)? Select one:

a. 0.5400
b. 0.5000
c. 0.7407
d. 0.8000

Answer 1

c. 0.7404

Explanation:

We can use Bayes Formula,

`P(N|C) = (P(C|N)*P(N))/(P(C))`

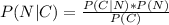
We know every single value of that expression except P(C). We can calculate C by dividing into 2 cases: if the customer is new or not.

By the total probability theorem, we know that P(C) = P(C|N)*P(N) + P(C|N')*P(N') = 0.5*0.8 + 0.7*0.2 = 0.4+0.14 = 0.54

We replace P(C) on the equation above and we obtain

`P(N|C) = (P(C|N)*P(N))/(P(C)) = (0.5*0.8)/(0.54) = 0.7407`

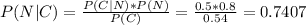
Thus, P(N|C) = 0.7407. Answer c is correct

I hope this helped you!