Question

In a physics lab, light with a wavelength of 490 nm travels in air from a laser to a photocell in a time of 16.6 ns. When a slab of glass with a thickness of 0.800 m is placed in the light beam, with the beam incident along the normal to the parallel faces of the slab, it takes the light a time of 21.0 ns to travel from the laser to the photocell. Use 3.00x108 m/s for the speed of light in a vacuum. Express your answer using two significant figures. O ? % AC 1 = 280 Submit Previous

Answer 1

The wavelength of the light in the glass is 182.9 nm.

Step-by-step explanation:

Given that,

Wavelength = 490 nm

Time = 16.6 ns

Thickness = 0.800 m

Suppose, we need to find the wavelength of the light in the glass.

We need to calculate the distance

Using formula of distance

`d=v* t`

`d=3*10^(8)*16.6*10^(-9)`

`d=4.98\ m`

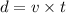
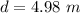
After slab,

We need to calculate the time to cross air

Using formula of time

`t=(d)/(v)`

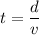
Put the value into the formula

`t=(4.98-0.800)/(3*10^(8))`

`t=13.9*10^(-9)\ s`

`t=13.9\ ns`

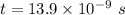
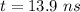
So the time in slab is

`t'=21.0-t`

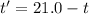
Put the value into the formula

`t'=21.0\ ns-13.9\ ns`

`t'=7.1\ ns`

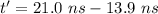
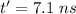
We need to calculate the speed in slab

Using formula of speed

`v=(0.8)/(t')`

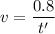
Put the value into the formula

`v=(0.8)/(7.1*10^(-9))`

`v=1.12*10^(8)\ m/s`

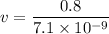
We need to calculate the wavelength

Using relation of wavelength and speed

`(c_(1))/(c_(2))=(\lambda_(1))/(\lambda_(2))`

Put the value into the formula

`(3*10^(8))/(1.12*10^(8))=(490*10^(-9))/(\lambda_(2))`

`\lambda_(2)=(490*10^(-9)*1.12*10^(8))/(3*10^(8))`

`\lambda_(2)=182.9\ nm`

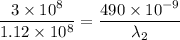
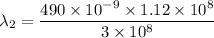
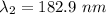
Hence, The wavelength of the light in the glass is 182.9 nm.