Answer:
Length=82
width= 46
Explanation:
Given:
Area of Rectangle}= 3772
Perimeter of Rectangle=256
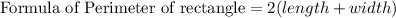
Substituting the values we get:
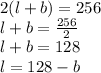
Now
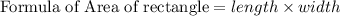
Substituting the values we get:
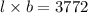
Now from above equation derived for length we will substitute value of l in the above equation we will get.
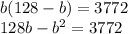
Now taking left hand side to right handside we get
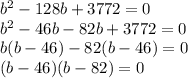
Now solving for both equation we get.
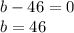
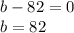
from above we can conclude that
length=82
width=46