Answer:
55.908 KN
Step-by-step explanation:
The ratio D/d=60/40=1.5
The ratio r/d=10/40=0.25
From the curve attached as missing part of the question and using the above two ratios we get concentration factor, k=1.6
Therefore,
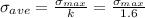
Since factor of safety, FS is given by
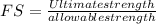
Allowable strength=
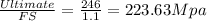
Substituting 223.63 Mpa for
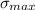 then for d=40 the stress is given by
then for d=40 the stress is given by
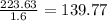
Also,
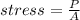 hence
hence

P=55.908 KN