The midpoint of Line AB is M(3, 3). The co-ordinates of B are (4, 7)
Solution:
Given that, the midpoint of Line AB is M(3, 3)
And the coordinates of A are (2, -1)
We have to find what are the coordinates of B
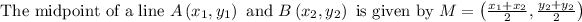
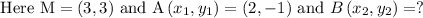
Substituting the values we get,
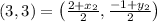
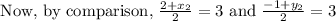
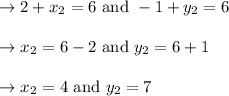
Hence, the co – ordinates of B is (4, 7)