Question

In a recent year, the average daily circulation of the Wall Street Journal was 2,276,207. Suppose the standard deviation is 70,940. Assume the paper’s daily circulation is normally distributed. (a) On what percentage of days would circulation pass 1,801,000? (b) Suppose the paper cannot support the fixed expenses of a full-production setup if the circulation drops below 1,611,000. If the probability of this even occurring is low, the production manager might try to keep the full crew in place and not disrupt operations. How often will this even happen, based on this historical information?

Answer 1

P ( percentage of days in which the circulation pass 1,801,000)

is equal to 100 % (almost)

P (percentage of days when the circulation drops below 1,611, 000)

is equal to 0 % (almost)

Explanation:

Let, in recent years, the daily circulation of the Wall Street Journal is given by the random variable X.

Then, according to the question,

X
`\sim` Normal (2,276,207 , 70,940)

let,

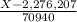`(X- 2,276,207)/(70940)` = Z

then Z
`\sim` Normal (0 , 1)

Now , for X = 1,801,000 , Z =
`(1,801,000- 2,276,207)/(70940)`

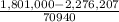
= -6.7 (approx)

Now, P ( percentage of days in which the circulation pass 1,801,000)

= P( Z > -6.7) = 100 % (almost)

So, P (percentage of days when the circulation drops below 1,611, 000)

= 0 % (almost) [ since, 1,801,000 > 1,611,000]