Answer:
One-fourth of the original gravitational force.
Step-by-step explanation:
The gravitational force between two objects of masses
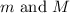 is given as:
is given as:
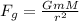
Where,

Therefore, the gravitational force is inversely proportional to the square of the distance between the masses.
Now, if the distance is doubled, then the force has to be reduced by a factor of one by four or gravitational force will one-fourth of the original.
Let us verify it.
If
 , then new gravitational force is,
, then new gravitational force is,
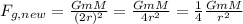
As seen above, new gravitational force is one-fourth of the original gravitational force between moon and Earth.