Question

In a pool game, the cue ball, which has an initial speed of 2 m/s, makes an elastic collision with the eight ball, which is initially at rest. The two balls have equal masses of 6 kg. After the collision, the eight ball moves at an an angle of 50.7 ◦ to the original direction of the cue ball.

Answer 1

The direction of motion of the cue ball is 39.3°.

Step-by-step explanation:

Given that,

Initial speed = 2 m/s

Two balls have equal masses = 6 kg

After the collision,

The eight ball moves at an angle of 50.7° to the original direction of the cue ball.

Suppose we need to calculate the direction of motion of the cue ball after the collision

We need to calculate the direction of motion of the cue ball

If the collision is elastic,

Using conservation of energy

`(1)/(2)m_(A)v_(iA)^2+(1)/(2)m_(B)v_(iB)^2=(1)/(2)m_(A)v_(fA)^2+(1)/(2)m_(B)v_(fB)^2`

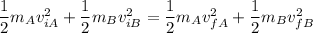
Where,
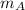`m_(A)` = mass of the cue ball

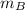`m_(B)`= mass of the eight ball

The two balls have equal masses.

So
`m_(A)=m_(B)`

`v_(iA)^2+0=v_(fA)^2+v_(fB)^2`

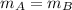
The angle of the cue ball after the collision

`\theta_(A)+\theta_(B)=90^(\circ)`

`\theta_(A)=90-\theta_(B)`

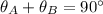
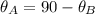
Put the value into the formula

`\theta_(A)=90-50.7`

`\theta_(A)=39.3^(\circ)`

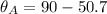
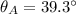
Hence, The direction of motion of the cue ball is 39.3°.