The total area of pyramid is 113.569 square units
The equation to find the total area of the pyramid is Total area = base area + lateral area.
Solution:
Given, A pyramid has a regular hexagonal base with side lengths of 4 and a slant height of 6.
The total area of pyramid is given by:
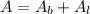 ---- eqn 1
---- eqn 1
Where,
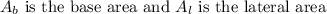
The area of base is given as:
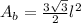
Where "l" is the side of hexagon.
Substituting we get,
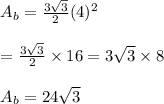
The lateral area is given as:

Where,
b: base of the triangle
h: height of the triangle
Substituting we get,

Plugging in the values we found in eqn 1 we get,
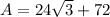
A = 113.569 square units
Summarizing the results:
The total area of pyramid is 113.569 square units approximately
The equation used to find total area of pyramid is Total area = base area + lateral area.