Answer:
- $0.47
Here, negative sign depicts the expected loss
Step-by-step explanation:
Data provided in the question:
Bet amount for number 24 = $9
Probability of winning on number 24 =
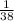
Award amount for number 24 = $315
Probability of losing on number 24 = 1 -
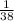 =
=
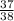
Losing amount = $9
Now,
The expected value of the game to the player
= Winning amount × Probability of winning - Losing amount × Probability of losing
= ( $315 ×
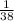 ) - ( $9 ×
) - ( $9 ×
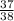 )
)
= 8.29 - 8.76
= - $0.47
Here, negative sign depicts the expected loss